Как решать с помощью кругов эйлера. Логические задачи и круги эйлера

Министерство образования, науки и молодежи Республики Крым Малая академия наук «Искатель»

Направление: математика

г. Красноперекопск – 2017

Работу выполнила:

Шумилина Мария Сергеевна,

ученица 7-А класса муниципального бюджетного общеобразовательного учреждения «Средняя общеобразовательная школа № 5» муниципального образования городской округ Красноперекопск

Научный руководитель:

Шеина Елена Николаевна, учитель математики муниципального бюджетного общеобразовательного учреждения «Средняя общеобразовательная школа № 5 » муниципального образования городской округ Красноперекопск

ВВЕДЕНИЕ …………………………………………………………… 3

ГЛАВА 1. Немного из истории…………………………………. 5

ГЛАВА 2. Из теории множеств……………………………………….7

2.1. Понятие множества.……………………………………..8

2.2. Операции над множествами. …………………………..9

ГЛАВА 3. Решение задач с помощью кругов Эйлера ………………..10

ЗАКЛЮЧЕНИЕ…………………………………………………………..22

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ ………………….23

ВВЕДЕНИЕ

Ничто так не способствует

формированию мыслительной культуры,

как решение логических задач. Математика-

не сухая и скучная наука, а полная

необычных и интересных открытий

Решать логические задачи очень увлекательно. Есть люди, для которых решение логической задачи - увлекательная, но несложная задача. Их мозг как луч прожектора сразу освещает все хитроумные построения, и к правильному ответу они приходят необычайно быстро. Замечательно, что при этом не могут объяснить, как пришли к решению.

Логические задачи составляют обширный класс нестандартных задач. Сюда относятся, прежде, всего, текстовые задачи, в которых требуется распознать объекты или расположить их в определенном порядке по имеющимся свойствам.

Существует множество приемов, которые используются при решении текстовых логических задач. Очень часто решение помогает найти рисунок. Использование рисунка делает решение задачи простым и наглядным. Изображение условий задачи в виде кругов Эйлера, как правило, упрощает и облегчает путь к её решению.

Актуальность состоит в том, что задачи имеют практический характер, что немаловажно в современной жизни. Задачи заставляют задумываться, подходить к решению какой-либо проблемы с другой стороны, уметь выбирать из множества способов решения, наиболее простой, легкий путь.

Цель работы:

Познакомится с кругами Эйлера – Венна;

Научиться применять способ решения задач с помощью кругов Эйлера;

Составлять задачи практического содержания.

Глава 1. Немного из истории

Леонард Эйлер, крупнейший математик XVIII в., родился в Швейцарии в 1707г. В 1727 г. по приглашению Петербургской академии наук он приехал в Россию. В Петербурге Эйлер попал в круг выдающихся ученых: математиков, физиков, астрономов, получил большие возможности для создания и издания своих трудов. Он работал с увлечением и вскоре стал, по единодушному признанию современников, первым математиком мира. Научное наследие Эйлера поражает своим объемом и разносторонностью. В списке его трудов более 800 названий. Полное собрание сочинений ученого занимает 72 тома. Среди его работ - первые учебники по дифференциальному и интегральному исчислению. В теории чисел Эйлер продолжил деятельность французского математика П. Ферма.

Эйлер много работает в области математического анализа. Ученый впервые разработал общее учение о логарифмической функции. В геометрии Эйлер положил начало совершенно новой области исследований, выросшей впоследствии в самостоятельную науку-топологию.

Имя Эйлера носит формула, связывающая число вершин (В), ребер (Р) и граней (Г) выпуклого многогранника: В -Р + Г = 2. Даже основные результаты научной деятельности Эйлера трудно перечислить. Здесь и геометрия кривых и поверхностей, и первое изложение вариационного исчисления с многочисленными новыми конкретными результатами. У него были труды по гидравлике, кораблестроению, артиллерии, геометрической оптике и даже по теории музыки. Он впервые дает аналитическое изложение механики вместо геометрического изложения Ньютона, строит механику твердого тела, а не только материальной точки или твердой пластины. Одно из самых замечательных достижений Эйлера связано с астрономией и небесной механикой. Он построил точную теорию движения Луны с учетом притяжения не только Земли, но и Солнца. Это пример решения очень трудной задачи.

Последние 17 лет жизни Эйлера были омрачены почти полной потерей зрения. Но он продолжал творить так же интенсивно, как в молодые годы. Только теперь он уже не писал сам, а диктовал ученикам, которые проводили за него наиболее громоздкие вычисления.

С1761 по 1768 год им были написаны знаменитые «Письма к немецкой принцессе», где Эйлер как раз и рассказывал о своем методе, об изображении множеств в виде кругов. Именно поэтому рисунки в виде кругов, обычно называют «кругами Эйлера». Эйлер отмечал, что изображение множеств в виде кругов «очень подходит для того, чтобы облегчить наши рассуждения».

После Эйлера этот же метод разрабатывал чешский математик Бернард Больцано (1781 – 1848). Только в отличие от Эйлера он рисовал не круговые, а прямоугольные схемы. Методом кругов Эйлера пользовался и немецкий математик Эрнст Шредер (1841 – 1902). Этот метод широко используется в его книге «Алгебра логика». Но наибольшего расцвета графические методы достигли в сочинениях английского логика Джона Венна (1843 – 1923). С наибольшей полнотой этот метод изложен им в книге «Символическая логика», изданной в Лондоне в 1881 году. В честь Венна вместо кругов Эйлера соответствующие рисунки называют иногда диаграммами Венна; в некоторых книгах их называют также диаграммами (или кругами) Эйлера – Венна.

Глава 2. Из теории множеств

2.1. Понятие множества.

Одним из основных понятий, которые используются в математике, является понятие множества. Для него не дается определения. Можно пояснить, что множеством называют произвольную совокупность объектов, а сами объекты – элементами данного множества. Так, можно говорить о множестве учеников в классе (элементы – ученики),множестве дней недели (элементы – дни недели), множестве натуральных делителей числа 6 (элементы – числа 1, 2, 3, 6) и т. д.

В курсах алгебры и алгебры начало анализа чаще всего рассматривают множества, элементами которых являются числа, и поэтому их называют числовыми множествами.

Как правило, множества обозначают прописными буквами латинского алфавита. Например, если множество M состоит из чисел 1; 2; 3, то его обозначают так: M = {1; 2; 3}. Тот факт, что число 2 входит в это множество

(является элементом данного множества M ) записывается с помощью специального значка следующим образом: 2 M ; а то что число 5 не входит в это множество (не является элементом данного множества M ), записывается так: 5 M .

Можно рассматривать также множество, не содержащее ни одного элемента, - пустое множество. Например: множество простых делителей числа 1 – пустое множество.

Для некоторых множеств существуют специальные обозначения. Так, пустое множество обозначается символом , множество всех натуральных чисел – буквой N , множество всех целых чисел – буквой Z , множество всех рациональных чисел – буквой Q , а множество всех действительных чисел буквой R . С помощью кругов Эйлера – Венна это можно изобразить так:

Рис.1

Если каждый элемент множества A является элементом множества B , то говорят, что множество A является подмножеством множества B .

Это записывают следующим образом: A B .

Рис.2

2.2. Операции над множествами.

Над множествами можно выполнять определенные действия: находить их пересечение, объединение. Дадим определение этих операций и проиллюстрируем их с помощью кругов.

Пересечением множеств A и B называют их общую часть, то есть множество C всех элементов, принадлежащих как множеству A , так и множеству B

Пересечение множеств обозначают знаком ∩ и записывают A ∩ B .

Рис.3

Объединением множеств A и B называют множество C , состоящее из всех элементов, принадлежащих хотя бы одному из этих множеств (A или B ). Объединение множеств обозначают знаком
и записывают A
B

Глава3. Решение задач с помощью Кругов Эйлера

Задача № 1.

Из 52 школьников 23 собирают значки, 35 собирают марки, а 16 - и значки, и марки.

Остальные не увлекаются коллекционированием. Сколько школьников не увлекаются коллекционированием.

Решение.

В условии этой задачи не так легко разобраться. Если сложить 23 и 35, то получится больше 52. Это объясняется тем, что некоторых школьников мы здесь учли дважды, а именно тех, которые собирают и значки, и марки.

чтобы легче решать задачу, представим ее данные на следующей схеме

Рис.5

На этой схеме большой круг означает всех школьников, о которых идёт речь. Круг З изображает школьников, собирающих значки (всего их 23), а круг М - школьников, собирающих марки (всего их 35). В пересечении кругов З и М стоит число 16 - это те, кто собирает и значки, и марки. Значит, только значки собирает 23 - 16 = 7 человек, только марки собирает 35 - 16 = 19 человек. Всего марки и значкисобирает19 + 7 + 16 = 42 человека. Остаётся 52 - 42 = 10 человек, не увлечённых коллекционированием. Это число можно вписать в свободное поле круга. Ответ: 10 человек.

Задача 2.

В классе 15 мальчиков. Из них 10 человек занимается волейболом и 9 баскетболом. Сколько мальчиков занимается и тем, и другим?

Решение.

Изобразим условие с помощью кругов Эйлера. Этот рисунок подсказывает нам рассуждения. Разберём это рассуждение и впишем нужное число в каждую из образовавшихся на диаграмме частей.

Пусть всеми видами спорта занимаются х мальчиков. Тогда только волейболом занимаются (10-х) мальчиков, а только баскетболом (9-х) мальчиков. Составим уравнение: 10-х + х+ 9-х=15, откуда х=4

10-х Б

х 9-х

Рис.6

Ответ: 4 человека.

Задача № 3.

Некоторые ребята из нашего класса любят ходить в кино. Известно, что 15 ребят смотрели фильм «Чучело», 11 человек – фильм «Выше неба», из них 6 смотрели и «Чучело», и «Выше неба». Сколько человек смотрели только фильм «Выше неба»?

Решение: Чертим два множества таким образом: 6 человек, которые смотрели фильмы «Чучело» и «Выше неба», помещаем в пересечение множеств.

15 – 6 = 9 – человек, которые смотрели только «Чучело».
11 – 6 = 5 – человек, которые смотрели только «Выше неба».

Получаем:

Рис.7

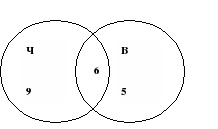
Ответ. 5 человек смотрели только «Выше неба».

Задача № 4.

В группе из 80 туристов, приехавших на экскурсию в Москву, 52 хотят посетить Большой театр, 30 - Художественный театр, 12 хотят посетить оба театра, остальные в театры ходить не хотят. Сколько человек не собирается идти в театр?

Решение.

Только большой театр посетят: 52-12=40 туристов;

только художественный театр посетят

30-12=18 туристов;

8
0-(40+18+12)=10 туристов не собираются идти в театр.

Рис.8

Ответ: 10 человек.

Задача № 5.

На полке стояло 26 волшебных книг по заклинаниям. Из них 4 прочитал и Гарри Поттер, и Рон. Гермиона прочитала 7 книг, которых не читали ни Гарри Поттер, ни Рон, и две книги, которые читал Гарри Поттер. Всего Гарри Поттер прочитал 11 книг. Сколько книг прочитал Рон?

Решение.

Учитывая условия задачи, чертеж будет таков:

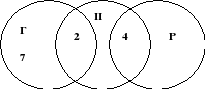
Рис.9

Так как Гарри Поттер всего прочитал 11 книг, из них 4 книги читал Рон и 2 книги – Гермиона, то 11 – 4 – 2 = 5 – книг прочитал только Гарри.

Следовательно, 26 – 7 – 2 – 5 – 4 = 8 – книг прочитал Рон. Ответ. 8 книг прочитал Рон.

Задача№6.

В туристической группе из 100 человек 75 человек знают немецкий язык, 65 человек - английский язык, а 10 человек - не знают ни немецкого, ни английского языка. Сколько туристов знают два языка? Решение.

Изобразим условие задачи в виде кругов Эйлера.

Легко видеть, что 90 туристов (100-10) знают хотя бы один язык; Пусть х туристов знают и английский, и немецкий языки. Тогда (65-х) туристов знают только английскй, а (75-х) человек только немецкий. Получим уравнение 65-х+75-х+х=90, откуда х=50 – туристов знают оба языка. Ответ: 50 туристов.

Задача№7.

Сколько человек участвует в прогулке, если известно, что 16 из них взяли бутерброд с ветчиной, 24 - с колбасой, 15 - с сыром, 11 и с ветчиной, и с колбасой, 8 и с ветчиной, и с сыром, 12 и с колбасой, и с сыром, 6-бутерброды всех видов, а 5- взяли пирожки? Решение : Изобразим множества следующим образом: Рис.11

16+24+15-11-8-12+6=30(чел) - участвовали в прогулке и с собой брали бутерброды или 3+2+6+5+7+6+1=30(чел)

30+5=35(чел) - участвовали в прогулке
Ответ. 35 человек

Задача №8

В 5 классе нашей школы 22, в 6 классе – 16, в 7 классе – 23 ребят. Известно, что кружки по лыжам, шахматам и спортивным играм ходят 4 человека. Каждые две секции посещают 9 человек. Сколько человек ходит из каждого класса на секции? Сколько учеников не ходит ни на какой спортивный кружок?

Решение. Если на все три кружка ходят 4 ученика, а на каждые два – 9 человек, то две секции с 5 и 6 класса, с 6 и 7 класса, с 5 и 7 класса посещают по 5

человек.

Рис.12

Получаем 5+5+4=14 пятиклассников посещают кружки, 22-14=8 человек не ходят ни на какой кружков. Рассуждая также, из шестиклассников 16-14=2 ученика никуда не ходя, а из семиклассников – 23-14=9 человек.

Ответ: 14 учеников с каждого класса посещают кружки, не ходят ни на какой из 5-ого – 7, из 6-ого – 2, из 7-ого – 9 учеников.

Задача № 9.

Из 100 ребят, отправляющихся в детский оздоровительный лагерь, кататься на сноуборде умеют 30 ребят, на скейтборде – 28, на роликах – 42. На скейтборде и на сноуборде умеют кататься 8 ребят, на скейтборде и на роликах – 10, на сноуборде и на роликах – 5, а на всех трех – 3. Сколько ребят не умеют кататься ни на сноуборде, ни на скейтборде, ни на роликах?

Решение: В оспользуемся кругами Эйлера.

Рис.13

Всеми тремя спортивными снарядами владеют три человека, значит, в общей части кругов вписываем число 3. На скейтборде и на роликах умеют кататься 10 человек, а 3 из них катаются еще и на сноуборде. Следовательно, кататься только на скейтборде и на роликах умеют 10-3=7 ребят. Аналогично получаем, что только на скейтборде и на сноуборде умеют кататься 8-3=5 ребят, а только на сноуборде и на роликах 5-3=2 человека. Внесем эти данные в соответствующие части. Определим теперь, сколько человек умеют кататься только на одном спортивном снаряде. Кататься на сноуборде умеют 30 человек, но 5+3+2=10 из них владеют и другими снарядами, следовательно, только на сноуборде умеют кататься 20 ребят. Аналогично получаем, что только на скейтборде умеют кататься 13 ребят, а только на роликах – 30 ребят. По условию задачи всего 100 ребят. 20+13+30+5+7+2+3=80 – ребят умеют кататься хотя бы на одном спортивном снаряде. Следовательно, 20 человек не умеют кататься ни на одном спортивном снаряде.
Ответ. 20 человек не умеют кататься ни на одном спортивном снаряде.

Задача № 10 .

В трёх седьмых классах 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют в хоре, не увлекаются спортом и не занимаются в драмкружке? Сколько ребят заняты только спортом?

Решение . Д - драмкружок; Х - хор; С - спорт. В круге Д - 27 ребят, в круге Х - 32 человека, в круге С - 22 ученика. Те 10 ребят из драмкружка, которые поют в хоре, окажутся в общей части кругов Д и X. Трое из них ещё и спортсмены, они окажутся в общей части всех трёх кругов. Остальные семеро спортом не увлекаются. Аналогично, 8-3=5

спортсменов, не поющих в хоре и 6-3=3, не посещающих драмкружок. Легко видеть, что 5+3+3=11 спортсменов посещают хор или драмкружок, 22-(5+3+3)=11 заняты только спортом; 70-(11+12+19+7+3+3+5)=10 - не поют в хоре, не занимаются в драмкружке, не увлекаются спортом.

Рис.14 Ответ: 10 человек.

Задача№11 . В классе 30 человек. 20 из них каждый день пользуются метро, 15 - автобусом, 23 - троллейбусом, 10 - и метро, и троллейбусом, 12 - и метро, и автобусом, 9 - и троллейбусом, и автобусом. Сколько человек ежедневно пользуются всеми тремя видами транспорта?

Решение.

Рис.15

Пусть х человек пользуется всеми тремя видами транспорта. Тогда пользуются только метро и троллейбусом - (10 − х) человек, только автобусом и троллейбусом - (9 − х) человек, только метро и автобусом -(12 − х) человек. Найдем, сколько человек пользуется одним только метро:

20 − (12 − х) − (10 − х) − х = х − 2

Аналогично получаем: х − 6 - только автобусом и х + 4 - только троллейбусом, так как всего 30 человек, составляем уравнение:

х + (12 − х) + (9 − х) + (10 − х) + (х + 4) + (х − 2) + (х − 6) = 30.

отсюда х = 3.

Ответ: 3 человека.

Задача № 12.

Из сотрудников фирмы 16 побывали во Франции,10-в Италии,6-в Англии; в Англии и Италии-5; в Англии и Франции -6; во всех трех странах - 5 сотрудников. Сколько человек посетили и Италию, и Францию, если всего в фирме работают 19 человек, и каждый из них побывал хотя бы в одной из названных стран?

Решение:

Нам известно, что во всех трех странах было 5 сотрудников. В Англии и Италии тоже 5, значит эти же сотрудники были и во Франции и поэтому в пересечении кругов А и И ставим 0. В Франции и Италии нам неизвестно поэтому пишем х-5 в пересечении кругов А и Ф. Т.к. в Англии было 6 человек, то 6-5-1=0 пишем 0,во Франции 16-х+5-6 и Италии 10-х+5-5 и всего в фирме 19 сотрудников, то остается составить и решить уравнение: 1+16-х+5-6+5+х-5+10-х+5-5=19, отсюда х=7, значит в Италии и Франции побывало 7-5=2 сотрудника фирмы.

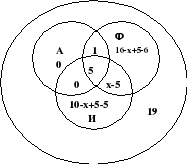
Рис.16

Ответ: 2 сотрудника.

Задача № 13.

Ребят, которые хотят обмениваться различного рода журналами, собралось 10 человек. Среди них выписывают К - 6 человек, Т – 5 человек, Ю – 5 человек, К и Т – 3 человека, Т и Ю -2 человека, К и Ю – 3 человека., а один человек не выписывает ни одного журнала., но читает все эти журналы в библиотеке. Надо узнать, сколько человек выписывают все три журнала, сколько – два, а сколько – только один журнал.

Решение. Пусть большой круг, состоящий из 10 человек, – это множество всех ребят, обменивающихся журналами. Внутри большого круга нарисуем три меньших круга: К, Т, Ю, которые изображают ребят, подписавшихся на соответствующие журналы.. Известно, что один человек не выписывает ни одного журнала.

Пусть х ребят выписывают все три журнала, тогда (3-х)ребят выписывают только К и Т, (2-х) –только Т и Ю, (3-х)- только К и Ю. Значит, только журнал К выписывают 6-(3-х+х+3-х)=х человек, журнал Т 5-(3-х+х+2-х)=х, журнал Ю 5-(3-х+х+2-х)=х.

Рис.17

Составим уравнение: х+3-х+3-х+х+х+х+х+2-х=9, 8+х=9,х=1

Итак, 3 – это число ребят, подписавшихся только на один журнал, 5 – это число ребят, подписавшихся на два журнала, а 1 – число ребят, подписавшихся на все три журнала.

ЗАКЛЮЧЕНИЕ

Предмет математики настолько серьезен,

что нельзя упускать случая сделать

его немного занимательным.

Б. Паскаль

Среди математических задач логические задачи занимают особое место Решение таких задач способствует развитию математического мышления. Они отличаются от большинства математических задач тем, что для их решения часто не требуется запас каких-то специальных знаний, а нужна, как правило, сообразительность. Одна из характерных черт любой логики состоит в том, что она позволяет, получив некоторую информацию, извлечь (выявить) содержащиеся в ней новые знания.

Оказывается приемов, с помощью которых можно решать текстовые логические задачи, несколько. Они разнообразны и каждый из них имеет свою область применения.

В моей работе рассмотрены задачи, которые состоят из множества данных. Найденные решения подчиняются одному и тому же способу: составляем рисунок; заносим первоначальные данные в круги; анализируя и рассуждая, записываем результаты в части кругов; ищем и записываем ответ. Изображение условий задачи в виде кругов Эйлера, как правило, упрощает и облегчает путь к её решению. Кроме того с их помощью можно ответить на множество вопросов, поставленных к одному условию задачи.

Данная тема расширила мой математический кругозор, обогатила арсенал средств, используемых в решении разнообразных задач.

Список используемых источников:

1. Гаврилова Т. Д..Занимательная математика. 5 - 11 классы. Волгоград: Учитель, 2005.-96 с.

2. Германович П.Ю. «Сборник задач по математике на сообразительность».

3. Гетманова А. Д. Логические основы математики 10 – 11 класс: учебное пособие. – М.: Дрофа, 2005.

4. Глейзер Г. И. . - М.: Просвещение, 1964. - С. 232.

5. Гусев В.А., Орлов А.И., Розенталь А.Л. «Внеклассная работа по математике». М.: Просвещение, 1984.

6. Нелин Е.П., Долгова О.Е.. Учебник алгебра и начала анализа 11 класс.

Тезисы к работе

Тема моей исследовательской работы «Решение задач с помощью кругов Эйлера ». При подготовке к олимпиаде я столкнулась с задачами, в которых большое количество данных. Оказывается, упростить решение таких задач помогают так называемые круги Эйлера, с помощью которых можно изобразить множество элементов, обладающих определённым свойством. Целью данной работы является изучение этого способа и умение применять его для решения задач.

В работе рассмотрены задачи, решение которых подчиняются одному алгоритму: составляем рисунок; заносим первоначальные данные в круги, начиная с условия которое содержит больше свойств; анализируя и рассуждая записываем результаты в части круга; записываем ответ.

Актуальность состоит в том, что задачи имеют практический характер, что немаловажно в современной жизни. Задачи заставляют задумываться, подходить к решению какой-либо проблемы с другой стороны, уметь выбирать из множества способов решения, наиболее простой, легкий путь. Способ, рассмотренный в работе доступен и легок в понимании, что позволяет расширить круг его применения. Круги Эйлера можно встретить и в истории, и в биологии, и при изучении других предметов.

Материал,который был исследован в работе,а также практическая часть, могут быть применены на дополнительных занятиях, при подготовке к математическим олимпиадам.

Логика. Учебное пособие Гусев Дмитрий Алексеевич

1.6. Круговые схемы Эйлера

Как мы уже знаем, в логике выделяется шесть вариантов отношений между понятиями. Два любых сравнимых понятия обязательно находятся в одном из этих отношений. Например, понятия писатель и россиянин находятся в отношении пересечения, писатель и человек – подчинения, Москва и столица России – равнозначности, Москва и Петербург – соподчинения, мокрая дорога и сухая дорога – противоположности, Антарктида и материк – подчинения, Антарктида и Африка – соподчинения и т. д. и т. п.

Надо обратить внимание на то, что если два понятия обозначают часть и целое, например месяц и год , то они находятся в отношении соподчинения, хотя может показаться, что между ними отношение подчинения, ведь месяц входит в год. Однако, если бы понятия месяц и год были подчиненными, то тогда надо было бы утверждать, что месяц – это обязательно год, а год – это не обязательно месяц (вспомним отношение подчинения на примере понятий карась и рыба : карась – это обязательно рыба, но рыба – это не обязательно карась). Месяц – это не год, а год – это не месяц, но и то, и другое – отрезок времени, следовательно, понятия месяц и год, так же, как и понятия книга и страница книги, автомобиль и колесо автомобиля, молекула и атом и т. п., находятся в отношении соподчинения, т. к. часть и целое – не то же самое, что вид и род.

В начале говорилось о том, что понятия бывают сравнимыми и несравнимыми. Считается, что рассмотренные шесть вариантов отношений применимы только к сравнимым понятиям. Однако возможно утверждать, что все несравнимые понятия находятся между собой в отношении соподчинения. Например, такие несравнимые понятия, как пингвин и небесное тело возможно рассматривать как соподчиненные, ведь пингвин – это не небесное тело и наоборот, но в то же время объемы понятий пингвин и небесное тело входят в более широкий объем третьего понятия, родового по отношению к ним: это может быть понятие объект окружающего мира или форма материи (ведь и пингвин и небесное тело – это различные объекты окружающего мира или различные формы материи). Если же одно понятие обозначает что-то материальное, а другое – нематериальное (например, дерево и мысль ), то родовым для этих (как возможно утверждать) соподчиненных понятий является понятие форма бытия , т. к. и дерево, и мысль, и что угодно еще – это различные формы бытия.

Как нам уже известно, отношения между понятиями изображаются круговыми схемами Эйлера. Причем до сих пор мы изображали схематично отношения между двумя понятиями, а это можно сделать и с большим количеством понятий. Например, отношения между понятиями боксер, негр и человек

Взаимное расположение кругов показывает, что понятия боксер и негр находятся в отношении пересечения (боксер может быть негром и может им не быть, а также негр может быть боксером и может им не быть), а понятия боксер и человек, так же как и понятия негр и человек находятся в отношении подчинения (ведь любой боксер и любой негр – это обязательно человек, но человек может не быть ни боксером, ни негром).

Рассмотрим отношения между понятиями дедушка, отец, мужчина, человек с помощью круговой схемы:

Как видим, указанные четыре понятия находятся в отношении последовательного подчинения: дедушка – это обязательно отец, а отец – не обязательно дедушка; любой отец – это обязательно мужчина, однако не всякий мужчина является отцом; и, наконец, мужчина – это обязательно человек, но человеком может быть не только мужчина. Отношения между понятиями хищник, рыба, акула, пиранья, щука, живое существо изображаются следующей схемой:

Попробуйте самостоятельно прокомментировать эту схему, установив все имеющиеся на ней виды отношений между понятиями.

Подытоживая сказанное, отметим, что отношения между понятиями – это отношения между их объемами. Значит, для того, чтобы было возможно установить отношения между понятиями, их объем должен быть резким, а содержание, соответственно, ясным, т. е. эти понятия должны быть определенными. Что касается неопределенных понятий, о которых шла речь выше, то установить точные отношения между ними достаточно сложно, фактически невозможно, ведь из-за неясности их содержания и нерезкости объема два каких-нибудь неопределенных понятия можно будет характеризовать как равнозначные или как пересекающиеся, или как подчиняющиеся и т. д. Например, возможно ли установить отношения между неопределенными понятиями неаккуратность и небрежность ? То ли это будет равнозначность, то ли подчинение – точно сказать невозможно. Таким образом, отношения между неопределенными понятиями являются так же неопределенными. Понятно поэтому, что в тех ситуациях интеллектуально-речевой практики, где требуется точность и однозначность в определении отношений между понятиями, использование неопределенных понятий является нежелательным.

Из книги Прозрение автора Ефимов Виктор Алексеевич

Из книги Философия науки и техники автора Стёпин Вячеслав Семенович

Теоретические схемы и абстрактные объекты технической теории Теоретические схемыпредставляют собой совокупность абстрактных объектов, ориентированных, с одной стороны, на применение соответствующего математического аппарата, а с другой, – на мысленный эксперимент,

Из книги Диалектика мифа автора Лосев Алексей Федорович

2. Диалектика схемы, аллегории и символа Какие же возможны вообще виды этого взаимоотношения? Их очень много. Но, следуя Шеллингу, можно указать три основных таких вида. При этом будем иметь в виду, что наши термины «внутреннее» и «внешнее» – очень общие термины и их можно

Из книги Курс эпохи Водолея. Апокалипсис или возрождение автора Ефимов Виктор Алексеевич

Из книги Избранные труды автора Щедровицкий Георгий Петрович

Из книги Человек среди учений автора Кротов Виктор Гаврилович

Комментарии и схемы Учение, в основе которого лежит внутренняя работа личности, не могло бы пережить саму эту личность без приливов новой внутренней работы новых личностей. Тех, кто увидел для себя особый смысл в этом учении. Меняются условия существования, приходит

Из книги Искусство правильно мыслить автора Ивин Александр Архипович

СХЕМЫ ПРАВИЛЬНЫХ РАССУЖДЕНИЙ Вот два примера дедуктивных выводов из рассказа русского юмориста начала века В. Билибина. «Если бы на свете не существовало солнца, то пришлось бы постоянно жечь свечи и керосин. Если бы пришлось постоянно жечь свечи и керосин, то чиновникам

Из книги Этика любви и метафизика своеволия: Проблемы нравственной философии. автора Давыдов Юрий Николаевич

Нравственная философия Толстого и Достоевского в рамках ницшеанской схемы нигилизма Начиная с последней четверти прошлого века проблема нигилизма выходит на одно из первых мест в числе важнейших проблем западноевропейской философии. Своим «статусом» она прежде всего

Из книги Нормы в пространстве языка автора Федяева Наталья Дмитриевна

2.1.1. Нормы-схемы речевого общения: речевой этикет Выбор первой проблемной области – речевого этикета – обусловлен следующим. При определении сущностных характеристик нормы мы начали движение от социальных норм, при этом заметили, что их существование в полной мере

Из книги Спиральная динамика [Управляя ценностями, лидерством и изменениями в XXI веке] автора Бек Дон

2.1.2. Семиотически закрепленные нормы-схемы: жанры Основой противопоставления социально и семиотически закрепленных норм, как было сказано в главе I, является способ их закрепления в социокультурной практике. Первые – неписаные законы – становятся программами, схемами

Из книги Логика и аргументация: Учебн. пособие для вузов. автора Рузавин Георгий Иванович

Из книги Архитектура и иконография. «Тело символа» в зеркале классической методологии автора Ванеян Степан С.

9.1. Графические схемы структуры аргументации Всякая аргументация начинается с установления и обсуждения некоторых фактов, которые в дальнейшем будут называться данными, и с помощью которых выдвигается и обосновывается некоторое заключение. Кроме того, для перехода от

Из книги автора

Иконография как система методов: схемы и угрозы Сама практика иконографического анализа сформировала «проверенную схему» последовательных исследовательских действий. Схема подразумевает:– уяснение исторического значения мотива – с точки зрения времени (момент

28 мая 2015

Леонард Эйлер (1707-1783) - известный швейцарский и российский математик, член Петербургской академии наук, бо́льшую часть жизни прожил в России. Наиболее известным в математическом анализе, статистике, информатике и логике считается круг Эйлера (диаграмма Эйлера-Венна), используемый для обозначения объема понятий и множеств элементов.

Джон Венн (1834-1923) - английский философ и логик, соавтор диаграммы Эйлера-Венна.

Совместимые и несовместимые понятия

Под понятием в логике подразумевается форма мышления, отражающая существенные признаки класса однородных предметов. Они обозначаются одним либо группой слов: «карта мира», «доминантовый квинтсептаккорд», «понедельник» и др.

В случае когда элементы объема одного понятия полностью или частично принадлежат объему другого, говорят о совместимых понятиях. Если же ни один элемент объема определенного понятия не принадлежит к объему другого, мы имеем место с несовместимыми понятиями.

В свою очередь, каждый из видов понятий имеет собственный набор возможных отношений. Для совместимых понятий это следующие:

тождество (равнозначность) объемов;
пересечение (частичное совпадение) объемов;
подчинение (субординация).

Для несовместимых:

соподчинение (координация);
противоположность (контрарность);
противоречие (контрадикторность).

Схематически отношения между понятиями в логике принято обозначать при помощи кругов Эйлера-Венна.

Отношения равнозначности

В данном случае понятия подразумевают один и тот же предмет. Соответственно, объемы данных понятий полностью совпадают. Например:

А - Зигмунд Фрейд;

В - основоположник психоанализа.

А - квадрат;

В - равносторонний прямоугольник;

С - равноугольный ромб.

Для обозначения используются полностью совпадающие круги Эйлера.

Пересечение (частичное совпадение)

А - педагог;

В - меломан.

Как видно из данного примера, объемы понятий частично совпадают: определенная группа педагогов может оказаться меломанами, и наоборот - среди меломанов могут быть представители педагогической профессии. Аналогичное отношение будет в случае, когда в качестве понятия А выступает, например, «горожанин», а в качестве В - «автоводитель».

Подчинение (субординация)

Схематически обозначаются как разные по масштабу круги Эйлера. Отношения между понятиями в данном случае характеризуются тем, что подчиненное понятие (меньшее по объему) полностью входит в состав подчиняющего (большего по объему). При этом подчиненное понятие не исчерпывает полностью подчиняющее.

Например:

А - дерево;

В - сосна.

Понятие В будет являться подчиненным по отношению к понятию А. Так как сосна относится к деревьям, то понятие А становится в данном примере подчиняющим, «поглощающим» объем понятия В.

Соподчинение (координация)

Отношение характеризует два и более понятия, исключающих друг друга, но принадлежащих при этом определенному общему родовому кругу. Например:

А - кларнет;

В - гитара;

С - скрипка;

D - музыкальный инструмент.

Понятия А, В, С не являются пересекающимися по отношению друг к другу, тем не менее, все они относятся к категории музыкальных инструментов (понятие D).

Противоположность (контрарность)

Противоположные отношения между понятиями подразумевают отнесенность данных понятий к одному и тому же роду. При этом одно из понятий обладает определенными свойствами (признаками), в то время как другое их отрицает, замещая противоположными по характеру. Таким образом, мы имеем дело с антонимами. Например:

А - карлик;

В - великан.

Круг Эйлера при противоположных отношениях между понятиями разделяется на три сегмента, первый из которых соответствует понятию А, второй - понятию В, а третий - всем остальным возможным понятиям.

Противоречие (контрадикторность)

В данном случае оба понятия представляют собой виды одного и того же рода. Как и в предыдущем примере, одно из понятий указывает на определенные качества (признаки), в то время как другое их отрицает. Однако, в отличие от отношения противоположности, второе, противоположное понятие, не заменяет отрицаемые свойства другими, альтернативными. Например:

А - сложная задача;

В - несложная задача (не-А).

Выражая объем понятий подобного рода, круг Эйлера разделяется на две части - третьего, промежуточного звена в данном случае не существует. Таким образом, понятия также являются антонимами. При этом одно из них (А) становится положительным (утверждающим какой-либо признак), а второе (В или не-А) - отрицательным (отрицающим соответствующий признак): «белая бумага» - «не белая бумага», «отечественная история» - «зарубежная история» и т. д.

Таким образом, соотношение объемов понятий по отношению друг к другу является ключевой характеристикой, определяющей круги Эйлера.

Отношения между множествами

Также следует различать понятия элементов и множества, объем которых отображают круги Эйлера. Понятие множества заимствовано из математической науки и имеет достаточно широкое значение. Примеры в логике и математике отображают его как некую совокупность объектов. Сами же объекты являются элементами данного множества. «Множество есть многое, мыслимое как единое» (Георг Кантор, основатель теории множеств).

Обозначение множеств осуществляется заглавными буквами: А, В, С, D… и т. д., элементов множеств - строчными: а, b, с, d…и др. Примерами множества могут быть студенты, находящиеся в одной аудитории, книги, стоящие на определенной полке (или, например, все книги в какой-либо определенной библиотеке), страницы в ежедневнике, ягоды на лесной поляне и т. д.

В свою очередь, если определенное множество не содержит ни одного элемента, то его называют пустым и обозначают знаком Ø. Например, множество точек пересечения параллельных прямых, множество решений уравнения х 2 = -5.

Решение задач

Для решения большого количества задач активно используются круги Эйлера. Примеры в логике наглядно демонстрируют связь логических операций с теорией множеств. При этом используются таблицы истинности понятий. Например, круг, обозначенный именем А, представляет собой область истинности. Таким образом, область вне круга будет представлять ложь. Чтобы определить область диаграммы для логической операции, следует заштриховать области, определяющие круг Эйлера, в которых ее значения для элементов А и В будут истинны.

Использование кругов Эйлера нашло широкое практическое применение в разных отраслях. Например, в ситуации с профессиональным выбором. Если субъект озабочен выбором будущей профессии, он может руководствоваться следующими критериями:

W - что я люблю делать?

D - что у меня получается?

P - чем я смогу хорошо зарабатывать?

Изобразим это в виде схемы: круги Эйлера (примеры в логике - отношение пересечения):

Результатом станут те профессии, которые окажутся на пересечении всех трех кругов.

Отдельное место круги Эйлера-Венна занимают в математике (теория множеств) при вычислении комбинаций и свойств. Круги Эйлера множества элементов заключены в изображении прямоугольника, обозначающего универсальное множество (U). Вместо кругов также могут использоваться другие замкнутые фигуры, но суть от этого не меняется. Фигуры пересекаются между собой, согласно условиям задачи (в наиболее общем случае). Также данные фигуры должны быть обозначены соответствующим образом. В качестве элементов рассматриваемых множеств могут выступать точки, расположенные внутри различных сегментов диаграммы. На ее основе можно заштриховать конкретные области, обозначив тем самым вновь образованные множества.

С данными множествами допустимо выполнение основных математических операций: сложение (сумма множеств элементов), вычитание (разность), умножение (произведение). Кроме того, благодаря диаграммам Эйлера-Венна можно проводить операции сравнения множеств по числу входящих в них элементов, не считая их.

Разделы: Информатика

1. Введение

В курсе Информатики и ИКТ основной и старшей школы рассматриваются такие важные темы как “Основы логики” и “Поиск информации в Интернет”. При решении определенного типа задач удобно использовать круги Эйлера (диаграммы Эйлера-Венна).

Математическая справка. Диаграммы Эйлера-Венна используются прежде всего в теории множеств как схематичное изображение всех возможных пересечений нескольких множеств. В общем случае они изображают все 2 n комбинаций n свойств. Например, при n=3 диаграмма Эйлера-Венна обычно изображается в виде трех кругов с центрами в вершинах равностороннего треугольника и одинаковым радиусом, приблизительно равным длине стороны треугольника.

2. Представление логических связок в поисковых запросах

При изучении темы “Поиск информации в Интернет” рассматриваются примеры поисковых запросов с использованием логических связок, аналогичным по смыслу союзам “и”, “или” русского языка. Смысл логических связок становится более понятным, если проиллюстрировать их с помощью графической схемы – кругов Эйлера (диаграмм Эйлера-Венна).

Логическая связка	Пример запроса	Пояснение	Круги Эйлера
& - “И”	Париж & университет	Будут отобраны все страницы, где упоминаются оба слова: Париж и университет	Рис.1
\| - “ИЛИ”	Париж \| университет	Будут отобраны все страницы, где упоминаются слова Париж и/или университет	Рис.2

3. Связь логических операций с теорией множеств

С помощью диаграмм Эйлера-Венна можно наглядно представить связь логических операций с теорией множеств. Для демонстрации можно воспользоваться слайдами в Приложение 1.

Логические операции задаются своими таблицами истинности. В Приложении 2 подробно рассматриваются графические иллюстрации логических операций вместе с их таблицами истинности. Поясним принцип построения диаграммы в общем случае. На диаграмме – область круга с именем А отображает истинность высказывания А (в теории множеств круг А – обозначение всех элементов, входящих в данное множество). Соответственно, область вне круга отображает значение “ложь” соответствующего высказывания. Что бы понять какая область диаграммы будет отображением логической операции нужно заштриховать только те области, в которых значения логической операции на наборах A и B равны “истина”.

Например, значение импликации равно “истина” в трех случаях (00, 01 и 11). Заштрихуем последовательно: 1) область вне двух пересекающихся кругов, которая соответствует значениям А=0, В=0; 2) область, относящуюся только к кругу В (полумесяц), которая соответствует значениям А=0, В=1; 3) область, относящуюся и к кругу А и к кругу В (пересечение) – соответствует значениям А=1, В=1. Объединение этих трех областей и будет графическим представлением логической операции импликации.

4. Использование кругов Эйлера при доказательстве логических равенств (законов)

Для того, чтобы доказать логические равенства можно применить метод диаграмм Эйлера-Венна. Докажем следующее равенство ¬(АvВ) = ¬А&¬В (закон де Моргана).

Для наглядного представления левой части равенства выполним последовательно: заштрихуем оба круга (применим дизъюнкцию) серым цветом, затем для отображения инверсии заштрихуем область за пределами кругов черным цветом:

Рис.3 Рис.4

Для визуального представления правой части равенства выполним последовательно: заштрихуем область для отображения инверсии (¬А) серым цветом и аналогично область ¬В также серым цветом; затем для отображения конъюнкции нужно взять пересечение этих серых областей (результат наложения представлен черным цветом):

Рис.5 Рис.6 Рис.7

Видим, что области для отображения левой и правой части равны. Что и требовалось доказать.

5. Задачи в формате ГИА и ЕГЭ по теме: “Поиск информации в Интернет”

Задача №18 из демо-версии ГИА 2013.

В таблице приведены запросы к поисковому серверу. Для каждого запроса указан его код – соответствующая буква от А до Г. Расположите коды запросов слева направо в порядке убывания количества страниц, которые найдет поисковый сервер по каждому запросу.

Код	Запрос
А	(Муха & Денежка) \| Самовар
Б	Муха & Денежка & Базар & Самовар
В	Муха \| Денежка \| Самовар
Г	Муха & Денежка & Самовар

Для каждого запроса построим диаграмму Эйлера-Венна:

Запрос А

Запрос Б

Запрос В

Запрос Г

Ответ: ВАГБ.

Задача В12 из демо-версии ЕГЭ-2013.

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

Запрос	Найдено страниц (в тысяч)
Фрегат \| Эсминец	3400
Фрегат & Эсминец	900
Фрегат	2100

Какое количество страниц (в тысячах) будет найдено по запросу Эсминец ?

Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

Ф – количество страниц (в тысячах) по запросу Фрегат ;

Э – количество страниц (в тысячах) по запросу Эсминец ;

Х – количество страниц (в тысячах) по запросу, в котором упоминается Фрегат и не упоминается Эсминец ;

У – количество страниц (в тысячах) по запросу, в котором упоминается Эсминец и не упоминается Фрегат.

Построим диаграммы Эйлера-Венна для каждого запроса:

Запрос	Диаграмма Эйлера-Венна	Количество страниц
Фрегат \| Эсминец	Рис.12	3400
Фрегат & Эсминец	Рис.13	900
Фрегат	Рис.14	2100
Эсминец	Рис.15	?

Согласно диаграммам имеем:

Х+900+У = Ф+У = 2100+У = 3400. Отсюда находим У = 3400-2100 = 1300.
Э = 900+У = 900+1300= 2200.

Ответ: 2200.

6. Решение логических содержательных задач методом диаграмм Эйлера-Венна

В классе 36 человек. Ученики этого класса посещают математический, физический и химический кружки, причем математический кружок посещают 18 человек, физический - 14 человек, химический - 10. Кроме того, известно, что 2 человека посещают все три кружка, 8 человек - и математический и физический, 5 и математический и химический, 3 - и физический и химический.

Сколько учеников класса не посещают никаких кружков?

Для решения данной задачи очень удобным и наглядным является использование кругов Эйлера.

Самый большой круг – множество всех учеников класса. Внутри круга три пересекающихся множества: членов математического (М ), физического (Ф ), химического (Х ) кружков.

Пусть МФХ – множество ребят, каждый из которых посещает все три кружка. МФ¬Х – множество ребят, каждый из которых посещает математический и физический кружки и не посещает химический. ¬М¬ФХ - множество ребят, каждый из которых посещает химический кружок и не посещает физический и математический кружки.

Аналогично введем множества: ¬МФХ, М¬ФХ, М¬Ф¬Х, ¬МФ¬Х, ¬М¬Ф¬Х.

Известно, что все три кружка посещают 2 человека, следовательно, в область МФХ впишем число 2. Т.к. 8 человек посещают и математический и физический кружки и среди них уже есть 2 человека, посещающих все три кружка, то в область МФ¬Х впишем 6 человек (8-2). Аналогично определим количество учащихся в остальных множествах:

Просуммируем количество человек по всем областям: 7+6+3+2+4+1+5=28. Следовательно, 28 человек из класса посещают кружки.

Значит, 36-28 = 8 учеников не посещают кружки.

После зимних каникул классный руководитель спросил, кто из ребят ходил в театр, кино или цирк. Оказалось, что из 36 учеников класса двое не были ни в кино. ни в театре, ни в цирке. В кино побывало 25 человек, в театре - 11, в цирке 17 человек; и в кино, и в театре - 6; и в кино и в цирке - 10; и в театре и в цирке - 4.

Сколько человек побывало и в кино, и в театре, и в цирке?

Пусть х – количество ребят, которые побывали и в кино, и в театре, и в цирке.

Тогда можно построить следующую диаграмму и посчитать количество ребят в каждой области:

В кино и театре побывало 6 чел., значит, только в кино и театре (6-х) чел.

Аналогично, только в кино и цирке (10-х) чел.

Только в театре и цирке (4-х) чел.

В кино побывало 25 чел., значит, из них только в кино были 25 - (10-х) – (6-х) – х = (9+х).

Аналогично, только в театре были (1+х) чел.

Только в цирке были (3+х) чел.

Не были в театре, кино и цирке – 2 чел.

Значит, 36-2=34 чел. побывали на мероприятиях.

С другой стороны можем просуммировать количество человек, которые были в театре, кино и цирке:

(9+х)+(1+х)+(3+х)+(10-х)+(6-х)+(4-х)+х = 34

Отсюда следует, что только один человек побывал на всех трех мероприятиях.

Таким образом, круги Эйлера (диаграммы Эйлера-Венна) находят практическое применение при решении задач в формате ЕГЭ и ГИА и при решении содержательных логических задач.

Литература

В.Ю. Лыскова, Е.А. Ракитина. Логика в информатике. М.: Информатика и Образование, 2006. 155 с.
Л.Л. Босова. Арифметические и логические основы ЭВМ. М.: Информатика и образование, 2000. 207 с.
Л.Л. Босова, А.Ю. Босова. Учебник. Информатика и ИКТ для 8 класса: БИНОМ. Лаборатория знаний, 2012. 220 с.
Л.Л. Босова, А.Ю. Босова. Учебник. Информатика и ИКТ для 9 класса: БИНОМ. Лаборатория знаний, 2012. 244 с.
Сайт ФИПИ: http://www.fipi.ru/

Леонард Эйлер – величайший из математиков,написал более 850 научных работ. В одной из них и появились эти круги.

Учёный писал, что «они очень подходят для того, чтобы облегчить наши размышления».

Круги Эйлера – это геометрическая схема, которая помогает находить и/или делать более наглядными логические связи между явлениями и понятиями. А также помогает изобразить отношения между каким-либо множеством и его частью.

Задача 1

Из 90 туристов, отправляющихся в путешествие, немецким языком владеют 30 человек, английским – 28 чел, французским – 42 чел. Английским и немецким одновременно владеют 8 человек, английским и французским -10 чел, немецким и французским – 5 чел, всеми тремя языками – 3 чел. Сколько туристов не владеют ни одним языком?

Решение:

Покажем условие задачи графически – с помощью трёх кругов

Ответ: 10 человек.

Задача 2

Многие ребята нашего класса любят футбол, баскетбол и волейбол. А некоторые - даже два или три из этих видов спорта. Известно, что 6 человек из класса играют только в волейбол, 2 – только в футбол, 5 – только в баскетбол. Только в волейбол и футбол умеют играть 3 человека, в футбол и баскетбол – 4, в волейбол и баскетбол – 2. Один человек из класса умеет играть во все игры, 7 не умеют играть ни в одну игру. Требуется найти:

Сколько всего человек в классе?

Сколько человек умеют играть в футбол?

Сколько человек умеют играть в волейбол?

Задача 3

В детском лагере отдыхало 70 ребят. Из них 20 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов, а 3 спортсмена посещают и драмкружок, и хор. Сколько ребят не поют в хоре, не увлекаются спортом и не занимаются в драмкружке? Сколько ребят заняты только спортом?

Задача 4

Из сотрудников фирмы 16 побывали во Франции, 10 – в Италии, 6 – в Англии. В Англии и Италии – пятеро, в Англии и Франции – 6, во всех трёх странах – 5 сотрудников. Сколько человек посетили и Италию, и Францию, если всего в фирме работает 19 человек, и каждый их них побывал хотя бы в одной из названных стран?

Задача 5

Шестиклассники заполняли анкету с вопросами об их любимых мультфильмах. Оказалось, что большинству из них нравятся «Белоснежка и семь гномов», «Губка Боб Квадратные Штаны» и «Волк и теленок». В классе 38 учеников. «Белоснежка и семь гномов» нравится 21 ученику. Причем трем среди них нравятся еще и «Волк и теленок», шестерым - «Губка Боб Квадратные Штаны», а один ребенок одинаково любит все три мультфильма. У «Волка и теленка» 13 фанатов, пятеро из которых назвали в анкете два мультфильма. Надо определить, скольким же шестиклассникам нравится «Губка Боб Квадратные Штаны».

Задачи для решения учащимися

1. В классе 35 учеников. Все они являются читателями школьной и районной библиотек. Из них 25 берут книги в школьной библиотеке, 20 - в районной. Сколько из них:

а) не являются читателями школьной библиотеки;

б) не являются читателями районной библиотеки;

в) являются читателями только школьной библиотеки;

г) являются читателями только районной библиотеки;

д) являются читателями обеих библиотек?

2.Каждый ученик в классе изучает английский или немецкий язык, или оба этих языка. Английский язык изучают 25 человек, немецкий - 27 человек, а тот и другой - 18 человек. Сколько всего учеников в классе?

3.На листе бумаги начертили круг площадью 78 см2 и квадрат площадью 55 см2. Площадь пересечения круга и квадрата равна 30 см2. Не занятая кругом и квадратом часть листа имеет площадь 150 см2. Найдите площадь листа.

4. В группе туристов 25 человек. Среди них 20 человек моложе 30 лет и 15 человек старше 20 лет. Может ли так быть? Если может, то в каком случае?

5. В детском саду 52 ребенка. Каждый из них любит пирожное или мороженое, или то и другое. Половина детей любит пирожное, а 20 человек - пирожное и мороженое. Сколько детей любит мороженое?

6. В классе 36 человек. Ученики этого класса посещают математический, физический и химический кружки, причем математический кружок посещают 18 человек, физический - 14, химический - 10. Кроме того, известно, что 2 человека посещают все три кружка, 8 человек -.и математический, и физический, 5 - и математический, и химический, 3 - и физический, и химический кружки. Сколько учеников класса не посещают никакие кружки?

7. После каникул классный руководитель спросил, кто из ребят ходил в театр, кино или цирк. Оказалось, что из 36 учеников двое не были ни в кино, ни в театре, ни в цирке. В кино побывали 25 человек; в театре - 11; в цирке - 17; и в кино, и в театре - 6; и в кино, и в цирке - 10; и в театре, и в цирке - 4. Сколько человек побывали в театре, кино и цирке одновременно?

Решение задач ЕГЭ с помощью кругов Эйлера

Задача 1

В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» - символ «&».

Крейсер & Линкор ? Считается, что все вопросы выполняются практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

Запрос	Найдено страниц (в тысячах)
Крейсер \| Линкор	7000
Крейсер	4800
Линкор	4500

Решение:

При помощи кругов Эйлера изобразим условия задачи. При этом цифры 1, 2 и 3 используем, чтобы обозначить полученные в итоге области.

Опираясь на условия задачи, составим уравнения:

Крейсер | Линкор: 1 + 2 + 3 = 7000
Крейсер: 1 + 2 = 4800
Линкор: 2 + 3 = 4500

Чтобы найти Крейсер & Линкор (обозначенный на чертеже как область 2), подставим уравнение (2) в уравнение (1) и выясним, что:

4800 + 3 = 7000, откуда получаем 3 = 2200.

Теперь этот результат мы можем подставить в уравнение (3) и выяснить, что:

2 + 2200 = 4500, откуда 2 = 2300.

Ответ: 2300 - количество страниц, найденных по запросу Крейсер & Линкор.

Задача 2

В языке запросов поискового сервера для обозначения

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

Запрос	Найдено страниц (в тысячах)
Торты \| Пироги	12000
Торты & Пироги	6500
Пироги	7700

Какое количество страниц (в тысячах) будет найдено по запросу Торты ?

Решение

Для решения задачи отобразим множества Тортов и Пирогов в виде кругов Эйлера.

А , Б , В ).

Из условия задачи следует:

Торты │Пироги = А + Б + В = 12000

Торты & Пироги = Б = 6500

Пироги = Б + В = 7700

Чтобы найти количество Тортов (Торты = А + Б ), надо найти сектор А Торты│Пироги ) отнимем множество Пироги.

Торты│Пироги – Пироги = А + Б + В -(Б + В ) = А = 1200 – 7700 = 4300

Сектор А равен 4300, следовательно

Торты = А + Б = 4300+6500 = 10800

Задача 3

|", а для логической операции "И" - символ "&".

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

Запрос	Найдено страниц (в тысячах)
Пироженое & Выпечка	5100
Пироженое	9700
Пироженое \| Выпечка	14200

Какое количество страниц (в тысячах) будет найдено по запросуВыпечка ?

Решение

Для решения задачи отобразим множества Пироженых и Выпечек в виде кругов Эйлера.

Обозначим каждый сектор отдельной буквой (А , Б , В ).

Из условия задачи следует:

Пироженое & Выпечка = Б = 5100

Пироженое = А + Б = 9700

Пироженое │ Выпечка = А + Б + В = 14200

Чтобы найти количество Выпечки (Выпечка = Б + В ), надо найти сектор В , для этого из общего множества (Пироженое │ Выпечка) отнимем множество Пироженое .

Пироженое │ Выпечка – Пироженное = А + Б + В -(А + Б ) = В = 14200–9700 = 4500

Сектор В равен 4500, следовательноВыпечка = Б + В = 4500+5100 = 9600

Задача 4
убывания
Для обозначения логической операции "ИЛИ" используется символ " |", а для логической операции "И" - символ "&".
Решение

Представим множества овчарок, терьеров и спаниелей в виде кругов Эйлера, обозначим сектора буквами (А , Б , В , Г ).

с паниели │(терьеры & овчарки) = Г + Б

с паниели│овчарки = Г + Б + В

спаниели│терьеры│овчарки = А + Б + В + Г

терьеры & овчарки = Б

Расположим номера запросов в порядке убывания количества страниц: 3 2 1 4

Задача 5

В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения логической операции "ИЛИ" используется символ " |", а для логической операции "И" - символ "&".

1	барокко \| классицизм \| ампир
2	барокко \| (классицизм & ампир)
3	классицизм & ампир
4	барокко \| классицизм

Решение

Представим множества классицизм, ампир и классицизм в виде кругов Эйлера, обозначим сектора буквами (А , Б , В , Г ).

Преобразим условие задачи в виде суммы секторов:

барокко│ классицизм │ампир = А + Б + В + Г
барокко │(классицизм & ампир) = Г + Б
классицизм & ампир = Б
барокко│ классицизм = Г + Б + А

Из сумм секторов мы видим какой запрос выдал больше количества страниц.

Расположим номера запросов в порядке возрастания количества страниц: 3 2 4 1

Задача 6
В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения логической операции "ИЛИ" используется символ " |", а для логической операции "И" - символ "&".

1	канарейки \| щеглы \| содержание
2	канарейки & содержание
3	канарейки & щеглы & содержание
4	разведение & содержание & канарейки & щеглы

Решение

Для решения задачи представим запросы в виде кругов Эйлера.

K - канарейки,

Щ – щеглы,

Р – разведение.

канарейки \| терьеры \| содержание	канарейки & содержание	канарейки & щеглы & содержание	разведение & содержание & канарейки & щеглы

Самая большая область закрашенных секторов у первого запроса, затем у второго, затем у третьего, а у четвертого запроса самый маленький.

В порядке возрастания по количеству страниц запросы будут представлены в следующем порядке: 4 3 2 1

Обратите внимание что в первом запросе закрашенные сектора кругов Эйлера содержат в себе закрашенные сектора второго запроса, а закрашенные сектора второго запроса содержат закрашенные сектора третьего запроса, закрашенные сектора третьего запроса содержат закрашенный сектор четвертого запроса.

Только при таких условиях мы можем быть уверены, что правильно решили задачу.

Задача 7 (ЕГЭ 2013)

В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» – символ «&».

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

Запрос	Найдено страниц (в тысячах)
Фрегат \| Эсминец	3400
Фрегат & Эсминец	900
Фрегат	2100

Какое количество страниц (в тысячах) будет найдено по запросу Эсминец ?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

1	барокко \| классицизм \| ампир
2	барокко \| (классицизм & ампир)
3	классицизм & ампир
4	барокко \| классицизм